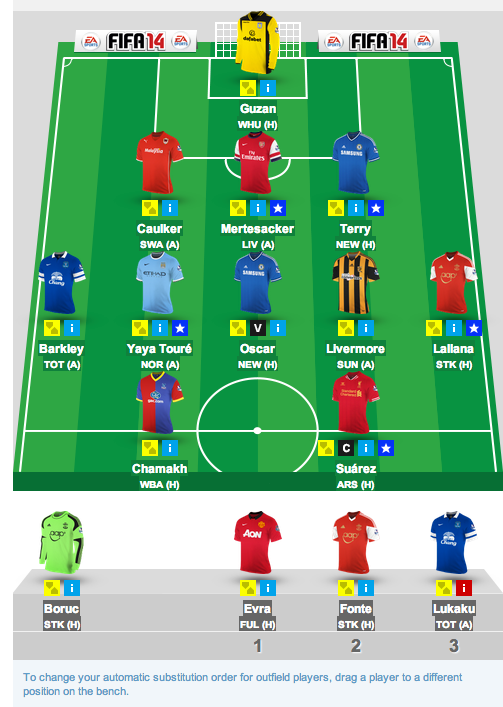
A couple months ago, my friend suckered me into a fantasy football league.
I like watching soccer, and we had watched a couple games together. I'd also played fantasy (American) football before, but I didn't have any idea how fantasy soccer worked.
I am competitive though, so I agreed to play and wanted to do well enough not to embarrass myself.
The first thing I had to do was to figure out how the game works.
In Fantasy Football, you have a team of 15 British Premier League players; 2 goalkeepers, 5 defenders, 5 midfielders, and 3 forwards.
Each week, you pick 11 starters and 4 subs. Your fantasy team scores points based on how well your players do: goals, assists, saves and preventing the other team from scoring all gain you fantasy points.
As you assemble your team, you have one big constraint: each player costs a certain amount of money, and you have a limited bankroll. So, to assemble your team, you want to choose the 15 players that will score the most points given that they cost less than your bank account.
The cost for each player ranges from about £4 to 14, based on how many other people have bought the player, and is not fixed. If a player scores more fantasy points, his price will go up; fewer and his price goes down.
Each week, you're allowed to trade out one of your players for a different player as long as you have enough money to buy the new player. Twice a season, you're allowed to play a wild card that allows you to trade out your entire team.
Once I'd picked up the rules, I started playing around with building up a team. I managed to build one manually, but it was a pain and I did so pretty poorly. I didn't really know the players, or the strategy, so I had to make some wild guesses.
A few weeks into the season, my team stunk, but I was getting the hang of things. I was frustrated that my team wasn't very good, so I decided to see if I could get my computer to pick a better team for me than the one I had picked myself.
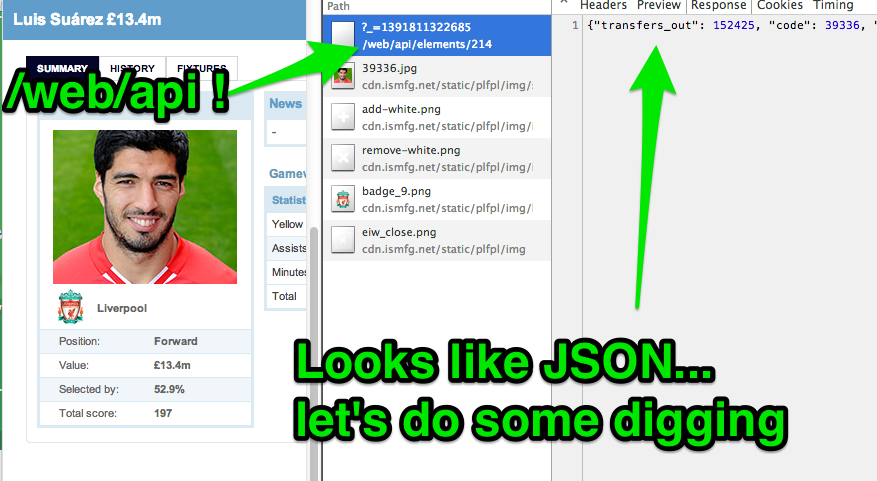
Once I'd decided I was going to use my computer, the first thing I needed to do is gather data for all the players in the Premier League. There's no official API, so I opened up my trusty Chrome inspector and did some digging.
After a brief search, I found an endpoint called /web/api, which looked like it output JSON. Awesome!
After I played with it a bit, I discovered that each player has an ID between 0 and 600, though some IDs are not taken. The endpoint is indeed JSON, so it's super simple to download and parse.
I wrote this little script to download every players' data, stick it in a dictionary, and save it to a file.
As you can see, it's very simple; it was a good thing I dug around and found that API so I didn't have to resort to screen scraping.
Now I was in a situation I find myself in frequently. I had an idea, I got all excited, went and downloaded data, but I needed to figure out how to get from the data to the answer I was looking for. Oftentimes, in the past, I'd end up with a directory full of half-finished scripts, and no answer.
website("http://ipython.org/notebook.html")
Enter: ipython notebook. Although it's reasonably new, ipython notebook has rapidly become my go-to tool for exploring data, generating graphs, and running experiments. It's great to keep all that stuff in one place, so you can see what work you've done and avoid having three different versions of a function in three different scripts. It also allows you to go back and edit the things you've done, leading to a very iterative style of development.
This talk, itself, is an ipython notebook converted into a slideshow.
If you're not familiar with the funny little "In" and "Out" notations on the left side, they indicate an ipython notebook cell. You write code in the "In" field, and see your output (no surprise here) in the "Out".
import cPickle
players = cPickle.load(open("players.data.pickle"))
scrolling_div(players[1])
I've created an ipython cell and loaded the player data that I downloaded with requests, then printed the first player's JSON data.
When you execute a cell in Ipython notebook, the variables you create are available for your use later on. Here, we've loaded the pickle file into a variable players, which we'll continue to use throughout the spreadsheet.
It looks like the object contains all the player information we need, primarily in a big fixture_history array that contains big, unlabelled, arrays. It contains their cost, the amount of points they've scored overall, their name, a list of all the games they've played, and a list of all their upcoming games.
%matplotlib inline
matplotlib.rc('font', size=18)
figsize(12, 4)
import numpy as np
import re
import StringIO
#import prettyplotlib as ppl
#dir(ppl)
points = {}
for p in players.itervalues():
for game in p['fixture_history']['all']:
if game[3] > 0:
points.setdefault(p['type_name'], []).append(game[19])
def poshist(axis, position):
axis.hist(points[position])
axis.set_title(position)
return axis
fig, (ax0, ax1, ax2, ax3) = plt.subplots(ncols=4, sharey=True, figsize=(18,4))
poshist(ax0, "Forward")
poshist(ax1, "Midfielder")
poshist(ax2, "Defender")
poshist(ax3, "Goalkeeper")
fig.show()
The first experiment I did asked: how many fantasy points are scored by players in each position?
So I wrote this code to iterate through all players, discard the games in which they didn't play, and store how many points they scored in a dictionary keyed on their position.
Then I used matplotlib to turn that dictionary into a series of four graphs.
This graph isn't that helpful, so don't bother squinting at it to find out what it says.
The point is that, with a very small amount of code, I was able to run an experiment, make graphs, and draw conclusions about my data.
IPython makes this all very easy by allowing you to rapidly iterate on your code, and showing you graphical output right next to your textual input. If you mess up, just fix the text in the cell, and run it again.
opponents = {}
for player in players.itervalues():
for game in player["fixture_history"]["all"]:
#skip games where the player played 0 minutes
if game[3] == 0: continue
opp = game[2][:3]
pts = game[19]
opponents.setdefault(opp, [0,0])[0] += pts
opponents[opp][1] += 1
from collections import OrderedDict
avgs = {}
for opponent, (score, n) in opponents.iteritems():
avgs[opponent] = score/float(n)
sorted_avgs = OrderedDict(sorted(avgs.items(), key=lambda t: t[1]))
fig, ax = plt.subplots(figsize=(18,4))
x_pos = np.arange(0, len(sorted_avgs.keys()))
ax.set_xticks(x_pos)
ax.set_xticklabels(sorted_avgs.keys(), rotation=45)
ax.plot(x_pos, sorted_avgs.values(), linewidth=3)
fig.show()
avg_opponent = sum(avgs.values())/float(len(avgs))
Next I asked another question: How many points does each team allow their opponents, on average?
So, again I iterated through all the player data. This time I saved the amount of points each player scored to a dictionary keyed by their opponent, then made a graph of the result.
I was impressed by the size of the effect: Liverpool, the stingiest team, gave up less than 2.2 fantasy points, on average, to their opponents. Fulham, the most generous, gave up nearly 4.
A game against the weakest team is worth nearly double, on average, to a game against the strongest!
This experiment demonstrated that a player's opponent in a fantasy game seems to be an important factor in how many points we can expect them to score in the future. We'll see later how this factors into our player model, and therefore what players the computer is going to select for us.
team_abbreviations = {
'Norwich': 'NOR',
'Cardiff City': 'CAR',
'Man City': 'MCI',
'Newcastle': 'NEW',
'West Brom': 'WBA',
'West Ham': 'WHU',
'Southampton': 'SOU',
'Sunderland': 'SUN',
'Stoke City': 'STK',
'Crystal Palace': 'CRY',
'Arsenal': 'ARS',
'Swansea': 'SWA',
'Liverpool': 'LIV',
'Hull City': 'HUL',
'Man Utd': 'MUN',
'Everton': 'EVE',
'Fulham': 'FUL',
'Tottenham': 'TOT',
'Aston Villa': 'AVL',
'Chelsea': 'CHE',
}
class Game(object):
def __init__(self, game_json):
self.opp = game_json[2][:3]
self.loc = game_json[2][4] # "A" for away, "H" for home
self.points = game_json[19]
self.minutes = game_json[3]
def __repr__(self):
return "Game vs. %s %s: %s pts" % (self.opp, self.loc, self.points)
class Player(object):
def __init__(self, player_json):
self.raw = player_json
self.games = [Game(g) for g in player_json["fixture_history"]["all"]]
self.name = u"{first_name} {second_name}".format(**player_json)
self.cost = player_json["event_cost"]
self.position = player_json["type_name"]
self.team = team_abbreviations[player_json["team_name"]]
self.idn = player_json["id"]
self.news = player_json["news"]
self.news_return = player_json["news_return"]
self.pos = self.shortname(self.position)
self.upcoming = self.get_upcoming_fixtures(player_json["fixtures"]["all"])
def get_upcoming_fixtures(self, fixtures):
upcoming = []
for _, gameweek, opponent in fixtures:
week = int(gameweek.split()[-1])
if opponent == "-":
continue
opp, loc = opponent.split('(')
opp = team_abbreviations[opp.strip()]
loc = loc[0]
upcoming.append((week, opp, loc))
return upcoming
def shortname(self, position):
pos_abbreviations = {
"Goalkeeper": "gk",
"Defender": "d",
"Midfielder": "m",
"Forward": "f"
}
return pos_abbreviations[position]
def __repr__(self):
return "#%s %s %s £%s %s" % (self.idn, self.team, self.name.encode("ascii", "ignore"), self.cost, self.pos)
def __unicode__(self):
return "#%s %s £%s %s" % (self.idn, self.name, self.cost, self.pos)
player_objs = [Player(p) for p in players.itervalues()]
def find_player(needle):
return [p for p in player_objs if needle.lower() in p.name.lower()]
Now I had the data loaded, and was able to quickly ask and answer questions, but I had all kinds of magic numbers in the code.
I needed to remember that a player's opponent is the 2nd field in a game array, his minutes is the 3rd, and his points is the 19th. It would be a lot nicer if I could wrap the player data in an object with convenient names for those fields.
So I went ahead and wrote a wrapper object that takes the JSON output from the Fantasy league API and turns it into a handy python object.
I don't want to go through this big hunk of code in detail, so instead I'll just tell you that the super nice thing about IPython Notebook is that you can code iteratively. When I actually created this code, it started as a very small and simple player class, with just his name, value, and points. As I needed more of the raw data, I went back to this cell in the notebook, edited the code, and re-ran it.
You don't have to get it right the first time, so it's very low stress.
p = find_player('Van Persie')[0]
print p.name
print p.position
print p.cost
print p.idn
print p.upcoming[:3] # upcoming games
print p.games[:3] # games he's already played
print p
Here I'm just playing around a bit with the player object I showed you in the previous slide. IPython auto-completes fields for me, so I can easily run quick sanity checks to make sure that I get the data I expect from the player object.
Each player now has attributes for his name, position, and cost, an array of past and upcoming games, and other important information. It's a big step up from the raw array we were using before.
homeaway = {"A": 0, "H": 0}
n = 0.
for player in player_objs:
#only consider full games to eliminate minute bias
for game in [p for p in player.games if p.minutes == 90]:
homeaway[game.loc] += game.points
n += 1
homeaway["A"] /= n
homeaway["H"] /= n
homefield = homeaway["H"] - homeaway["A"]
print homefield, homeaway
fig, ax = plt.subplots(figsize=(2,4))
x_pos = np.arange(0, len(homeaway.keys()))
ax.set_xticks(x_pos+.4)
ax.set_xticklabels(["Away", "Home"], rotation=45)
ax.bar(x_pos, homeaway.values())
fig.show()
Now it was even easier to run a third experiment: how valuable is homefield advantage?
So I wrote code to once again iterate through the players (using the objects this time), store their points in a dictionary keyed on whether the game was home or away, and display the results.
The result was that homefield advantage looks like it's worth about .3 fantasy points. Less important than who you play (which was worth almost 2 points, remember), but still worth thinking about.

At this point, I stopped playing around in IPython to think a bit. Now I had my players where I could get at them in a handy data structure, the ability to run experiments on them, and I'd found two important factors in predicting how many points they would score.
I knew that their opponent in upcoming games was very important, and whether the game was at home or away was important, but less so.
The next thing I needed to do was figure out a way to model a player's future predicted points.
Once I had that, I'd be most of the way to picking a team automatically. I'd just need to ask the computer to solve for a team that maximizes expected value while costing less than the amount of money I had to spend.
So I came up with a simple model, figuring that I could go back and change it if it didn't seem to generate a good team.
\(ev = \sum_{i=0}^5 opp_i + home_i + adj\_avg\)
In this simple model, each player's expected value is the sum of three factors.
The first is a factor to compensate for their opponent; they gain points is their opponent is generous and lose them if they're stingy.
The second is a factor for homefield advantage; a player gains expected fantasy points for being at home and loses them for being away.
The third is simply their past average score, adjusted for those same opponent and homefield advantage factors. So if their previous game was at home, we'd subtract some points which were presumably due to that homefield advantage. If it was away, we'd add them, hoping to neutralize its effect somewhat.
I chose to look 5 games into the future for each player when calculating their expected value. That was bascially just an off-the-cuff decision I made trying to look a bit into the future without projecting too far out.
This is a very simple model of player performance, and there's lots of things we could try to improve on, but it's a nice easy function to implement, that I figured would get me to a reasonable answer.
def adjusted_score(game):
pts = game.points
pts += homefield/2 if game.loc == "A" else -homefield/2
pts += avg_opponent - avgs[game.opp]
return pts
def adjusted_average(player):
return sum(adjusted_score(g) for g in player.games) / len(player.games)
def game_value(game):
adj = 0
adj += homefield/2 if game[2] == "H" else -homefield/2
adj += avgs[game[1]] - avg_opponent
return adj
def expected_points(player, n=5):
"""return the number of expected points in the next n games"""
av = adjusted_average(player)
ev = 0.
for game in player.upcoming[:n]:
ev += av + game_value(game)
return ev/n
print expected_points(find_player(u"Mutch")[0])
print expected_points(find_player(u"Suárez")[0])
print expected_points(find_player(u"Sanogo")[0])
# re-create our player objects, this time with our monkey-patched expected points function.
# In Real Life™, I would have just gone back to the player object and put it there, but that
# wouldn't make sense in this presentation, since I don't introduce the model until later.
Player.expected_points = expected_points
player_objs = [Player(p) for p in players.itervalues()]
player_objs[1].expected_points()
This code implements the model we just presented. It's easiest to read from the bottom up; let's start with expected_points.
This function takes a player, gets their adjusted average fantasy points for the season so far, then returns the average expected points of their next 5 games, adjusted for opponent and homefield advantage.
To do that adjustment, we have a pair of functions, adjusted_score and game_value, each of which simply takes a game and returns its adjusted value.
We run the expected_points function a couple of times at the end just to make sure it's sensible.
In this case, you see that Jordan Mutch is expected to score about 3 and a half points per game over the next 5 games, Luis Suárez 8, and the model expects that Yaya Sanogo is worth negative points. I went and looked at the scores those players have been posting, and who their upcoming opponents are, and those results seem reasonable given that information.
Given the constraints:
- Total player cost < 100
- 2 goalkeepers
- 5 defenders
- 5 midfielders
- 3 forwards
Maximize expected team value
So now we have a player model and it's time to construct a team. Let's look again at what we're trying to do.
I needed to pick a team of 15 players which costs less than £100 and fills up all the required player positions. Given those constraints, I wanted to pick the team that maximizes my expected fantasy point total.
This sort of problem, where we're trying to maximize or minimize some quantity with regard to a series of linear constraints is known as a linear optimization problem.
I had planned to use Scipy to solve the problem, but they don't have a very simple way to solve problems like this. Instead, after some googling, I turned to the special-purpose lp_solve program.
Given this simple optimization problem:
x1 >= 1 x2 >= 1 x1 + x2 >= 2 minimize x1 + x2 where x1 is an integer
Let's start by giving ourselves a very simple linear optimization problem, and solving it with lp_solve.
Take a look at this problem, and take a second to understand it. We have three constraints:
- x1 >= 1
- x2 >= 1
- x1 + x2 >= 2
and we want to minimize the sum of x1 + x2 given those constraints.
It should be clear the sum of x1 and x2 is minimized when x1 == x2 == 1.
lp_solve takes a file that looks like:
min: x1 + x2; x1 >= 1; x2 >= 1; x1 + x2 >= 2; int x1, x2;
Which, when run, results in:
$ lp_solve /tmp/simple_example Value of objective function: 2.00000000 Actual values of the variables: x1 1 x2 1
To solve this problem with lp_solve, we create a file in lp_solve format, as shown on the top here. It starts by telling lp_solve what function to minimize or maximize, and follows it with a series of constraints; one per line. Finally, we declare the type of all the variables we've used.
When we run lp_solve, it parses the file, minimizes the function we've given it, and returns the value of each variable.
max: 5.6 gk1 + 4.3 mf2 + …; /* maximize expected points */ 3.7 gk1 + 9.3 mf2 + … < 100; /* team must cost <100£ */ gk1 + gk12 + gk34 + … = 2; /* limit to 2 goalkeepers */ d3 + d4 + d23 + … = 5; /* limit to 5 defenders */ … /* repeat for all positions */ bin gk1, mf2, d3, f4, d5, …; /* all variables are binary */
The file I ended up passing to lp_solve isn't a whole lot different from that simple example; I just translated the fantasy football problem into a maximization problem using the values we already discussed.
The value we want to maximize is the expected point total of the players we choose.
The first constraint is our cost constraint; we want to make sure we can afford to buy the team the program picks.
Then there are four constraints, one for each position; we limit lp_solve to choosing 2 goalkeepers, 5 defenders, 5 midfielders, and 3 forwards.
lp_solve supports binary variables, so I made a variable to represent each player in the data set, consisting of their position and id number. For example, if player 2 is a midfielder, he'll be represented by mf2, as above.
The output of lp_solve would be a 1 if the player was selected for the team and a zero if they weren't.
That's why we're able to simply add up the player counts to get the position constraints; the player is a 1 if they've been selected and a zero otherwise.
def objective_function():
m = " + ".join("{ev} {p.pos}{p.idn}".format(p=p, ev=p.expected_points())
for p in player_objs)
return "max: " + m + ";\n"
So my next step was to create the lp_solve file
First, I wrote a function to output a maximization criteria. All it does is iterate through all players and join each player together, weighted by their expected point value.
This creates the expression lp_solve will be trying to maximize.
def cost_constraint(max_price):
c = " + ".join("{p.cost} {p.pos}{p.idn}".format(p=p)
for p in player_objs)
return "cost_constraint: " + c + " <= %s;\n" % max_price
Next, I wrote a very similar function to add a cost constraint. Again it loops through all players, but this time it weights them by their cost.
def position_constraints():
constraints = StringIO.StringIO()
gks = [p for p in player_objs if p.position == "Goalkeeper"]
gk_list = " + ".join(("gk{p.idn}".format(**locals()) for p in gks))
constraints.write("gk_limit: " + gk_list + " = 2;\n")
ds = [p for p in player_objs if p.position == "Defender"]
d_list = " + ".join(("d{p.idn}".format(**locals()) for p in ds))
constraints.write("d_limit: " + d_list + " = 5;\n")
ms = [p for p in player_objs if p.position == "Midfielder"]
m_list = " + ".join(("m{p.idn}".format(**locals()) for p in ms))
constraints.write("m_limit: " + m_list + " = 5;\n")
fs = [p for p in player_objs if p.position == "Forward"]
f_list = " + ".join(("f{p.idn}".format(**locals()) for p in fs))
constraints.write("f_limit: " + f_list + " = 3;\n")
return constraints.getvalue()
Finally, we add a constraint for each position. This code writes four constraints, which together limit the solver to choosing 2 goalkeepers, 5 defenders, 5 midfielders, and 3 forwards.
It does so by building a list of each player at each position, and limiting the sum of that position to the appropriate number.
Each player variable is a binary value; 1 if they're on the team or 0 if they're not, so the ability to add them up to limit the number of players comes in handy.
#create a buffer to hold all the constraints
buf = StringIO.StringIO()
buf.write(objective_function())
buf.write(cost_constraint(1000))
buf.write(position_constraints())
# I've skipped this, it's probably easier to skip the declaration of all the variable names?
# not very exciting
def all_player_variables():
variables = ", ".join("{p.pos}{p.idn}".format(**locals()) for p in player_objs)
return "bin %s;\n" % variables
buf.write(all_player_variables())
import subprocess, re
def get_player(idn):
"""given an id, return a player"""
for p in player_objs:
if p.idn == idn: return p
raise ValueError("Unable to find player")
def return_team(lp):
"""run lp_solve and return a list of player objects"""
cmd = "echo '%s' | lp_solve" % lp
val = subprocess.check_output(cmd, shell=True).split('\n')
get_id = lambda l: int(re.search("^\w+?(\d+)", l).group(1))
team_ids = [get_id(l) for l in val if re.search(r" 1$", l)]
return map(get_player, team_ids)
return_team(buf.getvalue())
Finally we take our constraints, pass them to lp_solve, parse the results, and it outputs a team!
Some improvments immediately suggest themselves; for example, lp_solve has chosen 5 players from the same team.
After tweaking the model and the constraints a bit, I took the team selected by lp_solve and put it into play. How'd it do?

The results were... OK. The computer definitely chose a better team than I had, but by the time I used it I had dug myself a pretty big hole.
It doesn't help that I'm more interested in writing code than I am in maintaining my fantasy football team, so I think I'm going to have to kiss my $5 goodbye.
In exchange though, I had a lot of fun playing around with ipython, solved a fun problem, and ended up with a talk. Not a bad outcome.
Thanks.